Los limites y el infinito

Muy buen día a todos y todas, hoy se hablara de los limites y el infinito, tal como pone el titulo, pero primero hablaremos del infinito ya que es algo bastante intrigante y de seguro causa curiosidad en mas de uno.

que es el infinito ? un siclo sin fin , una linea sin inicio ni terminación, al ser humano siempre le ha interesado lo eterno desde la antigüedad buscando fuentes para la vida eterna o con el sueño de obtener materiales sin fin ni costo .eso lo tenemos algo claro, pero ¿ que mas podemos saber de lo que literalmente es todo ? aquí unos cuantos datos sobre el infinito y algunos personajes que lo estudiaron.

El símbolo del infinito 

El símbolo del infinito que conocemos en a actualidad nación en el siglo XVII y su forma se da por el símbolo matemático llamado Lemiscata de Berneuilli . aunque en la latiguead aproximadamente en el 1600 a.c estese era representado como un circulo o la famosa serpiente que se muerde la cola.

El infinito es lo mas grande que puede densar el ser humano, pero que tan grande ?. En el cuerpo humano hay 10^17 células, y en un juego de ajedrez hay por lo menos 10^10^50 jugadas posibles, de por si estos números son gigantes , de echo existe un numero mas grande que estos y eses es el Numero Leviantan ( 10^666! ) el echo de pensar en este numero es de por si algo agobiante , y aunque este es extremadamente grande no es nada a comparación del infinito.

Georg Cantor  

Aunque nació en San Petersburgo (Rusia) — a donde sus padres habían emigrado desde Dinamarca—, Georg Cantor (1845-1918) pasó la mayor parte de su vida en Alemania. El infinito le interesó desde joven, y siendo un treintañero publicó los artículos que desarrollaron su Teoría de conjuntos, en la que formalizó diversas ideas sobre el infinito matemático. Des-afortunadamente su enfermedad mental ( maníaco-depresivo) lo obligaba a estar internado largos tiempos en una clínica mental aunque este tiempo era aprovechado para desarrollar sus teorías sobre el infinito.

Cantor fu el primero en dar una explicación matemática al infinito (ya que este se aplaca en mas de un ámbito ) y explico la existencia de varios infinito no solo uno, por ejemplo, los números del 1,2,3... y las secuencia 10,20,30... estas tienen la misma cantidad y sucede asi porque podemos emparejarlos, es decir ambos infinitos tienen el mismo tamaño.

De igual forma se pueden emparejar los infinitos de los enteros con los infinitos de las fracciones.

Hilbert y el hotel infinito 

Hilbert propuso un problema o dilema sobre un hotel infinito, la cuestión era la siguiente alguien llega a un hotel y pide una habitación, quien lo atiende le dice que si tienen una disponible aunque sabe que todas estan ocupadas, la solución era mover al huésped de la habitación 1 a la numero 2 , al de la 2 a la 3 y asi sucesivamente, de esta manera la habitación numero 1 siempre esta disponible para el nuevo huésped .


el concepto de infinito es de suma importancia para el mundo moderno ya que con este se dan los avances tecnológicos y lo relacionado con el mundo de la computación, también para el calculo como seria el calculo infinitesimal.



Hablemos de topologia
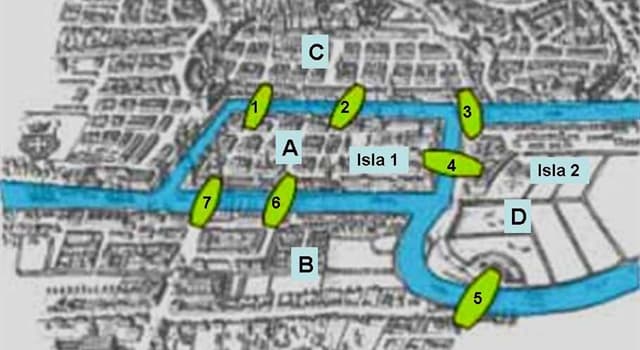Konigsberg planteo un problema, el problema de los 7 puentes de Konigsberg. se tenia que trazar una
ruta que pasara por los 7 puentes sin repetir el mismo dos veces,
Este problema fue resuelto por el matemático Leonhard Euler, quien demostró que no era posible, no importa la distancia entre los puentes si no la forma en que estén distribuidos.

Este problema dio origen a la topologia que se usa hoy en dia por ejemplo en los mapas de metro , ya que no importa que tan larga sea la uta si no como se distribuyen.

La geometría topográfica permite determinar la ubicación de un objeto y también su elevación .


Los limites 
Los limites se definen como el concepto de una función, cuando este se acerque a un valor determinado, es decir de forma aproximada. el limite es la división física o simbólica que marca una separación. 

Los limites se aplican en varias ramas por ejemplo:

Economía: para saber el valor máximo o mínimo que puede adquirir nuestro dinero en el mercado financiero

Química: para saber delas reacciones de concentración, se usa en la nanotecnologia para saber los limites llevar cada sustancia.

Medicina: para la creación de medicamentos determina los limites de cada sustancia para no causar efectos colaterales.

Construcción: para saber los limites del tipo de material y determinar cual es mas apto para el trabajo a ejercer.

Estadística: para saber el rango limite de una muestra.

Física: para determinar el área de gráficas curvas de movimiento.

En la vida cotidiana aplicamos constantemente los limites, por ejemplo el los juegos con pelota hacemos un calculo metal para determinar la trayectoria y posición final de este y asi atraparla, también estas los estudios de población en donde se estudian los limites de tiempo en os cuales crece la población .
Incluso se aplican en las redes sociales o tecnología, por ejemplo el numero máximo de caracteres que se pueden usar en alguna red social o el limite de caracteres para una contraseña o nombre de usuario.

Teorema de Bolzano 
Tienes que hacer un recorrido por un único camino, con las siguientes condiciones tienes que salir a las nueve del punto base y llegar al punto final a las 12 , el viaje lo haces como quieras, puedes correr o descansar lo que desees pero tienes que llegar a las 12. Cuando ya llegas a la meta descansas un día y esta vez regresas al punto base ( osea partes del punto final ) sales del punto final a las 9 y tienes que estar en e punto inicial a as 12.
Si sobreponemos estos recorridos, sin importar cuanto descansaste o corriste, existirá un punto en el que estos dos se encuentren 

Aquí dejo un vídeo racionado con los limites y en el cual se explica de buena forma este teorema.

¿De cuantas lados podemos inscribir un polígono regular para poder hallar el perímetro de la
circunferencia?

El polígono inscrito en la circunferencia tendría infinitos lados y el limite seria la circunferencia, esto es porque para encintar mas fácil el área de una circunferencia creamos dentro de esta una figura recta, y cada vez aumentamos el numero de lados de esta, y llegan a ser infinitos pero se toma una cantidad de lados aproximada.

Arquimides y la corona 

Arquimides fue un físico de la antigua Grecia al cual se le encomendó un importante tarea, tenia que  

determinar si la corona del rey fue echa con oro puro o si este se mezclo con un material mas barato.Rumorea que la idea que uso para resolver este problemas le llego cuando se estaba bañando, al notar que el agua se desbordo de la gran tina, se percato que esa cantidad de agua era el volumen de su cuerpo.

Posterior a esto, Arquimides tomo la corona y un trozo de oro del mismo peso y si la corona era de oro puro los dos objetos tendrían que desplazar la misma cantidad de agua. La corona desplazo mas asi que fue mezclada con otro material.

Primera computadora analógica

Fue encontrada fragmentada en Grecia, bajo el mar s dice que se utilizaba para medir y determinar las pociones planetarias predecir eclipses lunares y solares con 19 años de antelación, he incluso mostrar las fechas de algunos juegos olímpicos. Estese es como un complejo mecanismo de relojería y se encontraron 82 fragmentos y se recupero en 1900

Por que lo barcos flotan ?

Esto nos lo eplica el principio de Arquimides, este dice que todo objeto sumergido en un fluido sea liquido o gas experimenta una fuerza de empuje hacia arriba equivalente al volumen del liquido desplazado. Por esto a la hora de crear un barco se debe tener en cuenta que el peso del barco sea igual al volumen de agua desplazada, esto se logra a partir del diseño del barco.

Las palancas 

La palanca es la maquina mas sencilla y una de las mas antiguas tiene sus orígenes o antecedentes en Arquimides, esta conformada por tres partes, la carga , la fuerza y el punto de apoyo o fulcro , la distancia entre la fuerza y la carga recibe el nombre de brazos de palanca.

Existen tres tipos de palancas que se distinguen entre si por la posición de la fuerza, la carga y el punto de apoyo:

De primer tipo: el punto de apoyo se encuentra entre la carga y la fuerza 

De segundo tipo: la carga esta entre el punto de apoyo y la fuerza, ente mas largo sea el brazo de palanca de la fuerza con respecto al brazo de palanca de la carga , se reduce el esfuerzo para levantar o comprimir una carga como ocurre con la carretilla de mano.

De tercer tipo: la fuerza esta entre el punto de apoyo y la carga.

tornillo de Arquímedes 

Un tornillo de Arquímedes es una máquina gravimétrica helicoidal utilizada para la elevación de agua, harina, cereales o material excavado. Fue inventado en el siglo III a. C. por Arquímedes, del que recibe su nombre, aunque existen hipótesis de que ya era utilizado en el Antiguo Egipto.

Además de su uso en los sistemas de regadío, también fue utilizado para la recuperación de tierra en los Países Bajos entre otros. Se obtiene la tierra del mar y el agua que trae se bombea fuera del área cerrada, comenzando el proceso de drenaje de la tierra para su uso en la agricultura.

Es utilizado en las plantas de tratamiento de aguas residuales, ya que deben lidiar con diferentes tasas de flujo y con sólidos en suspensión. Hacen uso de él aparatos como sopladores de nieve o los elevadores de grano. Encontramos el mismo principio aplicado en las piscifactorías donde los usan para levantar los peces de forma segura y transportarlos a otro sitio. De esta forma se evita la manipulación física de los peces.