Los limites y el infinito

Muy buen día a todos y todas, hoy se hablara de los limites y el infinito, tal como pone el titulo, pero primero hablaremos del infinito ya que es algo bastante intrigante y de seguro causa curiosidad en mas de uno.

que es el infinito ? un siclo sin fin , una linea sin inicio ni terminación, al ser humano siempre le ha interesado lo eterno desde la antigüedad buscando fuentes para la vida eterna o con el sueño de obtener materiales sin fin ni costo .eso lo tenemos algo claro, pero ¿ que mas podemos saber de lo que literalmente es todo ? aquí unos cuantos datos sobre el infinito y algunos personajes que lo estudiaron.

El símbolo del infinito 

El símbolo del infinito que conocemos en a actualidad nación en el siglo XVII y su forma se da por el símbolo matemático llamado Lemiscata de Berneuilli . aunque en la latiguead aproximadamente en el 1600 a.c estese era representado como un circulo o la famosa serpiente que se muerde la cola.

El infinito es lo mas grande que puede densar el ser humano, pero que tan grande ?. En el cuerpo humano hay 10^17 células, y en un juego de ajedrez hay por lo menos 10^10^50 jugadas posibles, de por si estos números son gigantes , de echo existe un numero mas grande que estos y eses es el Numero Leviantan ( 10^666! ) el echo de pensar en este numero es de por si algo agobiante , y aunque este es extremadamente grande no es nada a comparación del infinito.

Georg Cantor  

Aunque nació en San Petersburgo (Rusia) — a donde sus padres habían emigrado desde Dinamarca—, Georg Cantor (1845-1918) pasó la mayor parte de su vida en Alemania. El infinito le interesó desde joven, y siendo un treintañero publicó los artículos que desarrollaron su Teoría de conjuntos, en la que formalizó diversas ideas sobre el infinito matemático. Des-afortunadamente su enfermedad mental ( maníaco-depresivo) lo obligaba a estar internado largos tiempos en una clínica mental aunque este tiempo era aprovechado para desarrollar sus teorías sobre el infinito.

Cantor fu el primero en dar una explicación matemática al infinito (ya que este se aplaca en mas de un ámbito ) y explico la existencia de varios infinito no solo uno, por ejemplo, los números del 1,2,3... y las secuencia 10,20,30... estas tienen la misma cantidad y sucede asi porque podemos emparejarlos, es decir ambos infinitos tienen el mismo tamaño.

De igual forma se pueden emparejar los infinitos de los enteros con los infinitos de las fracciones.

Hilbert y el hotel infinito 

Hilbert propuso un problema o dilema sobre un hotel infinito, la cuestión era la siguiente alguien llega a un hotel y pide una habitación, quien lo atiende le dice que si tienen una disponible aunque sabe que todas estan ocupadas, la solución era mover al huésped de la habitación 1 a la numero 2 , al de la 2 a la 3 y asi sucesivamente, de esta manera la habitación numero 1 siempre esta disponible para el nuevo huésped .


el concepto de infinito es de suma importancia para el mundo moderno ya que con este se dan los avances tecnológicos y lo relacionado con el mundo de la computación, también para el calculo como seria el calculo infinitesimal.



Hablemos de topologia
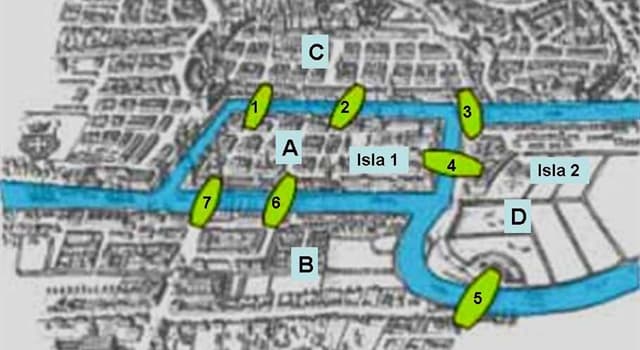Konigsberg planteo un problema, el problema de los 7 puentes de Konigsberg. se tenia que trazar una
ruta que pasara por los 7 puentes sin repetir el mismo dos veces,
Este problema fue resuelto por el matemático Leonhard Euler, quien demostró que no era posible, no importa la distancia entre los puentes si no la forma en que estén distribuidos.

Este problema dio origen a la topologia que se usa hoy en dia por ejemplo en los mapas de metro , ya que no importa que tan larga sea la uta si no como se distribuyen.

La geometría topográfica permite determinar la ubicación de un objeto y también su elevación .


Los limites 
Los limites se definen como el concepto de una función, cuando este se acerque a un valor determinado, es decir de forma aproximada. el limite es la división física o simbólica que marca una separación. 

Los limites se aplican en varias ramas por ejemplo:

Economía: para saber el valor máximo o mínimo que puede adquirir nuestro dinero en el mercado financiero

Química: para saber delas reacciones de concentración, se usa en la nanotecnologia para saber los limites llevar cada sustancia.

Medicina: para la creación de medicamentos determina los limites de cada sustancia para no causar efectos colaterales.

Construcción: para saber los limites del tipo de material y determinar cual es mas apto para el trabajo a ejercer.

Estadística: para saber el rango limite de una muestra.

Física: para determinar el área de gráficas curvas de movimiento.

En la vida cotidiana aplicamos constantemente los limites, por ejemplo el los juegos con pelota hacemos un calculo metal para determinar la trayectoria y posición final de este y asi atraparla, también estas los estudios de población en donde se estudian los limites de tiempo en os cuales crece la población .
Incluso se aplican en las redes sociales o tecnología, por ejemplo el numero máximo de caracteres que se pueden usar en alguna red social o el limite de caracteres para una contraseña o nombre de usuario.

Teorema de Bolzano 
Tienes que hacer un recorrido por un único camino, con las siguientes condiciones tienes que salir a las nueve del punto base y llegar al punto final a las 12 , el viaje lo haces como quieras, puedes correr o descansar lo que desees pero tienes que llegar a las 12. Cuando ya llegas a la meta descansas un día y esta vez regresas al punto base ( osea partes del punto final ) sales del punto final a las 9 y tienes que estar en e punto inicial a as 12.
Si sobreponemos estos recorridos, sin importar cuanto descansaste o corriste, existirá un punto en el que estos dos se encuentren 

Aquí dejo un vídeo racionado con los limites y en el cual se explica de buena forma este teorema.

¿De cuantas lados podemos inscribir un polígono regular para poder hallar el perímetro de la
circunferencia?

El polígono inscrito en la circunferencia tendría infinitos lados y el limite seria la circunferencia, esto es porque para encintar mas fácil el área de una circunferencia creamos dentro de esta una figura recta, y cada vez aumentamos el numero de lados de esta, y llegan a ser infinitos pero se toma una cantidad de lados aproximada.

Trabajo mecanico

Muy buen día a todos ( si es que alguien ve esto ), esta semana el trabajo estará relacionado con el movimiento mecánico  y la conservación de la energía. asi que  directamente iniciemos.

LAS INCREÍBLE FÍSICA Y LA PELEA DEL CALCULO

Buen día a todos , como ya mencione este blog esta echo para la resolución de trabajos durante la cuarentena por el covid-19, pero quizá la información le pueda servir a otras personas no vinculadas a mi institución educativa ( no creo que nadie mas lo vea , pero bueno ). En todo caso , a empezar con la información.

A por cierto tengo que aclarar que utilice de guía y como base para responder la actividad el libro "LA EVOLUCIÓN DE LA FÍSICA" de Albert Einstein y Leopold Infeld , junto con unos cuantos vídeos que probablemente dejare al final o en alguna parte del blog por si es de su interés.

Iniciemos

En los vídeos podemos notar que la principal motivación de Newton y Leibniz fue el mundo en movimiento , que era a su vez la principal preocupación Y Lde la época, ambos buscaron el modo de calcular la velocidad de un objeto móvil en determinado momento usando para esto los diferenciales.

precisamente estos dos físicos y matemáticos (entre sus otras múltiples disciplinas) tuvieron una fuerte contienda por el crédito de este descubrimiento hablemos un poco de cada uno: 

Isaac Newton

Nacio el 4 de enero de 1643 en Inglaterra. La infancia de newton fue bastante complicada , antes de su nacimiento su padre había fallecido, y nació de forma prematura,

su madre se caso nuevamente , pero el no tenia una buena relación con sus hermanastros ni su padrastro. Su madre lo abandonaría con su abuela posteriormente.

Newton seria entonces un niño introvertido y curioso con el mundo que lo rodeaba, realizaba experimentos relacionados con la luz pues llamaba mucho su atención .

Fue un físico, matemático, teólogo, inventor y alquimista cuyos experimentos, descubrimientos o aportes mas importantes  fueron :

     La ley de la gravedad, 

     la refracción de la luz  

     las leyes del movimiento 

junto con el calculo ya que newton fue considerado el fundador de este, el cual (como ya mencione antes) causo una disputa entre Leibniz y Newton.

Gottfied Leibniz

Fue un filosofo y matemático ingles. Su padre, profesor de filosofía moral en la universidad Leipzig falleció cunando este tenia seis años . Leibinz era capas de escribir poemas en latín a la corta edad de 8 años , posteriormente empresaria a interesarle por la lógica y matemática.

Las contribuciones de Leibniz en el campo del cálculo infinitesimal, efectuadas con independencia de los trabajos de Newton, así como en el ámbito del análisis combinatorio, fueron de enorme valor. Introdujo la notación actualmente utilizada en el cálculo diferencial e integral. Los trabajos que inició en su juventud, la búsqueda de un lenguaje perfecto que reformara toda la ciencia y permitiese convertir la lógica en un cálculo, acabaron por desempeñar un papel decisivo en la fundación de la moderna lógica simbólica.

Leibniz fue acusado por plagio, puesto que el y Newton se jactaron de la creación del calculo, esto metió en problemas a Leibniz pues Newton había trabajado ya este tema 10 años atrás, posterior a un juicio se llego a la conclusión de que  Newton era el primer fundador del calculo y Leibniz el segundo fundador. Esto lo afecto bastante pero aun asi siguió y dedico su vida al calculo , de echo las formulas métodos y expresiones que pendemos en la escuela sobre el calculo son los propuestos por Leibniz.

¿QUIEN FUE BERNOULLI Y EN PARA QUE FUE SU RETO? 

fue matemático, estadístico, físico y médico. Nació en Groningen, Holanda.  Este personaje realizo una especie de prueba o reto que envió a algunos matemáticos y físicos reconocidos de la época  entre los cuales estaban precisamente Newton y Leibniz , obviamente la carta que contenía la pregunta tardo en llegar pues en esa época  la comunicación era bastante lenta, pero bueno, la pregunta era la siguiente ,tenemos 2 puntos ,A y B ( el punto A se encuentra en lo alto, digamos en una torre y el punto B esta en el piso ) la pregunta era ¿ que curva haría que una bola se moviera del punto A al punto B usando la gravedad y en el menor tiempo posible?
Leibniz fue el primero en responder , y aunque Bernoulli tenia un plazo de tiempo fijado para la entrega de una respuesta, decidió extenderlo al no recibir respuesta del filosofo y físico por el que hizo esta pregunta , exactamente, este era Issac Newton , quien mando su respuesta sin firmar, pero aun asi Bernoulli supo de inmediato que esta era su respuesta.
El reto de Bernoulli estaba directamente relacionado con el comflicto entre Leibniz y Newton, la hizo para probar lo que cada un sabia de las cicloides. En resolución del problema la bola cae mas rápido siguiendo un curva cicloide que una linea recta si ellos conocían esta respuesta y solucionaron bien el problema , esto significaba que sabían sobre calculo. 

A, SI ....QUE BIEN

Muy buen día encuarentenados, en este bloc y como " magnifica, eficiente y estupenda estrategia " para continuar nuestros estudios se publicaran las soluciones de algunas actividades de la institución en que estudio , específicamente de las áreas matemáticas y física  " genial" ¿no?.